Kolmogorov–Smirnov test (K-S test) merupakan pengujian statistik non-parametric yang paling mendasar dan paling banyak digunakan, pertama kali diperkenalkan dalam makalahnya Andrey Nikolaevich Kolmogorov pada tahun 1933[1] dan kemudian ditabulasikan oleh Nikolai Vasilyevich Smirnov pada tahun 1948[2] . K-S test dimanfaatkan untuk uji satu sampel (one-sample test) yang memungkinkan perbandingan suatu distribusi frekuensi dengan beberapa distribusi terkenal, seperti distribusi normal Gaussian (Stephens, 1992; Biswas, Ahmad, Molla, Hirose & Nasser, 2008).
Konsep dasar K-S test hampir sama dengan uji normalitas yang pernah saya tulis (lihat: Uji Normalitas dengan Geary’s Test), yaitu mengukur perbandingan data empirik dengan data berdistribusi normal teoritik yang memiliki mean dan standar deviasi yang sama dengan data empirik. Menurut Kolmogorov (1992), suatu fungsi distribusi empirik (EDF, empirical distribution function) Fn(x) didefinisikan sebagai relasi-relasi
| Fn(x) = 0, | x < X1; | ||||
| Fn(x) = k / n, | Xk ≤ x < Xk + 1, | k = 1, 2, . . . , n – 1; | |||
| Fn(x) = 1, | Xn ≤ x. |
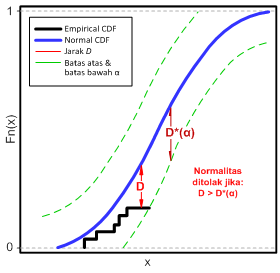
Gambar 1. Jarak vertikal D pada grafik
Kolmogorov–Smirnov test
K-S test mengukur kedekatan jarak antara F(x) dengan Fn(x) ketika n diasumsikan sebagai nilai yang sangat besar, Kolmogorov (1992) mendefinisikan fungsi distribusi kumulatifnya atau CDF (cumulative distribution function) adalah sebagai berikut:
D = supx |Fn(x) – F(x)|
yang mana supx adalah supremum dari sejumlah jarak D.
Secara grafik, D adalah jarak vertikal terjauh antara Fn(x) dan F(x). Nilai D ini selanjutnya dibandingkan dengan nilai D*(α) kritis dari sebuah tabel statistik untuk pengujian α (lihat Gambar 1).
Umumnya, para peneliti akan menggunakan software SPSS untuk uji normalitas dengan K-S test. Dalam posting ini, kita akan mencoba memakai free software PSPP karena output maupun perintah-perintahnya dinilai hampir sama dengan software populer SPSS.
Pengolahan Data
Pada langkah-langkah uji normalitas ini, saya menganggap para pembaca posting ini sudah paham dasar-dasar penggunaan SPSS, jika belum silahkan baca posting saya yang berjudul: Dasar-Dasar SPSS dan Statistik Deskriptif dengan SPSS. Selain free software PSPP, persiapkan juga tabel statistik K-S One-Sample Test untuk pengujian α. Berikut langkah-langkahnya:
- Data yang digunakan adalah data yang sama seperti pada Uji Normalitas dengan Geary’s Test, lihat Tabel 1.
| Tabel 1 |
| Contoh Hasil Pengamatan Time Study |
|
|
- Klik menu [Analyze] -> [Non-Parametric Statistics] -> [1-Sample K-S], lihat Gambar 2.

|
*) Perhatikan menu di atas, menu PSPP untuk K-S test bernama “Non-Parametric Statistics”, biasanya menu ini pada SPSS bernama “Nonparametric Tests” |
Gambar 2. Menu Kolmogorov–Smirnov Test
- Muncul dialog box One-Sample Kolmogorov -Smirnov Test. Klik variabel yang akan diuji ‐> klik
 untuk memasukkan variabel tersebut ke form Test Variable List.
untuk memasukkan variabel tersebut ke form Test Variable List. - Pilih distribusi normal dengan mencentang Normal pada form Test Distribution, lihat Gambar 3.
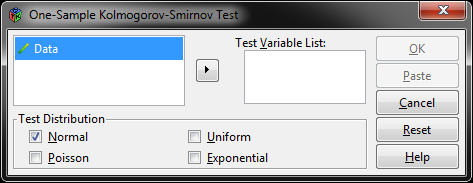
Gambar 3. Dialog Box Kolmogorov–Smirnov Test
- Terakhir klik [OK] dan hasilnya akan terlihat seperti Gambar 4 di bawah ini.

Gambar 4. Output Kolmogorov–Smirnov Test
Analisis
Tabel output pada Gambar 4 di atas menunjukkan N = 30 yang berarti jumlah sampel yang diambil sebanyak 30, mean = 1,83 yang berarti nilai rata-rata sampel X untuk menghampiri mean populasi μ, dan standar deviasi = 0,19. Terdapat tiga angka penting dalam tabel output tersebut:
Pertama, nilai-nilai D pada Most Extreme Differences.
Kedua, uji statistik Kolmogorov-Smirnov Z, yang mana dalam output sampel Z = 0,78.
Ketiga, p-value yang tercantum sebagai Asymp. Sig. (2-tailed), yang mana dalam kasus ini p-value = 0,58 .
Bagaimana menafsirkannya? Simak analisisnya di bawah ini.
1. Most Extreme Differences
Most Extreme Differences merupakan nilai statistik D pada K-S test, terdiri dari:
- D Positive ( D+ = supx [Fn(x) – F(x)] ) , merupakan pengurangan yang menghasilkan angka positif terbesar.
- D Negative ( D– = supx [F(x) – Fn(x)] ) , merupakan pengurangan yang menghasilkan angka negatif terbesar.
- D Absolute ( D = max {D+, D–} ) , merupakan angka terbesar antara nilai absolut D+ dan D–. Pada kasus ini D = 0,14.
K-S test menggunakan pengujian α dengan membandingkan nilai D Absolute dengan nilai D* kritis dari sebuah tabel statistik. Dengan menggunakan:
Hipotesis:
H0 : data mengikuti distribusi normal
H1 : data tidak mengikuti distribusi normal
Level of significance: α = 0,05
Kriteria Uji: H0 ditolak jika D > D*(α)
Nilai D hitung adalah sebesar 0,14 dan nilai D* (α = 0,05, n = 30) yang diperoleh dari tabel statistik adalah sebesar 0,242. Oleh karena 0,14 < 0,242 atau D < D*(α) maka H0 diterima yang berarti data mengikuti distribusi normal.
Secara visual K-S test diperlihatkan Gambar 5 di bawah ini, di mana kita menggambarkan CDF hipotesis pada sebuah grafik kemudian kurva jarak D di atas dan di bawah kurva hipotesis. Jika D (garis merah) keluar garis batas level of significance α (garis hijau), maka dapat disimpulkan bahwa data empirik (garis hitam) tidak mengikuti distribusi normal (lihat juga: Massey, 1951, pp. 69–71).
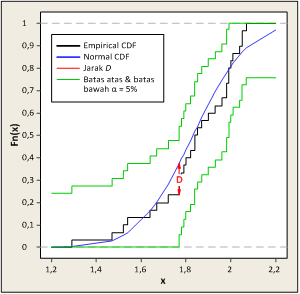
Gambar 5. Grafik ECDF untuk Kolmogorov–Smirnov test
2. Kolmogorov-Smirnov Z
Kolmogorov-Smirnov Z merupakan hasil dari akar kuadrat dari jumlah sampel N dan perbedaan absolut terbesar antara CDF empiris dan CDF teoritis (Yu, Zheng, Zhao & Zheng, 2008, p. 138), ini hampir sama dengan akar kuadrat dari jumlah sampel N dikali D Absolute:
Z ≈ √N x D Absolute
Menurut Brito e Abreu & Goulão (2001), “Kolmogorov-Smirnov Z” adalah D Absolute yang diubah menjadi sebuah standardized score (p. 52), yang dimaksud standardized score adalah nilai Z dalam distribusi normal standar. Artinya, cara pengujiannya hampir sama dengan pengujian nilai D, hanya saja kali ini di bawah distribusi normal dengan menggunakan bantuan tabel distribusi normal standar, yang mana:
H0 ditolak jika Z-hitung (Kolmogorov-Smirnov) > Z-tabel pada level of significance α.
Kita mempunyai Z-hitung (Kolmogorov-Smirnov) = 0,78 dengan memilih level of significance α = 0,05 pada dua ujung wilayah kritis (the two-sided critical region), Z-tabel pada tabel distribusi normal standar adalah 1,96. Oleh karena 0,78 < 1,96 atau Z-hitung (Kolmogorov-Smirnov) < Z-tabel, maka H0 diterima yang berarti data mengikuti distribusi normal.
3. Asymp. Sig. (2-tailed)
Asymptotic significance 2-tailed merupakan pengujian nilai probability atau p-value untuk memastikan bahwa distribusi teramati tidak akan menyimpang secara signifikan dari distribusi yang diharapkan di kedua ujung two-tailed distribution (Yu, Zheng, Zhao & Zheng, 2008, p. 138).
Menurut Corder dan Foreman (2009), p-value ini dapat dicari dengan menggunakan formula Smirnov (1948) setelah nilai Kolmogorov-Smirnov Z diketahui, yaitu sebagai berikut (p. 27):
| Jika 0 | ≤ | Z | < | 0,27 | ; | p = 1 | |
| Jika 0,27 | ≤ | Z | < | 1 | ; | p = 1 − [(2,506628 / Z) (Q1 + Q19 + Q125)] | |
| Jika 1 | ≤ | Z | < | 3,1 | ; | p = 2(Q2 − Q24 + Q29 − Q216) | |
| Jika | Z | ≥ | 3,1 | ; | p = 0 |
yang mana Q1 = e−1.233701(Z−2) dan Q2 = e−2(Z2).
Kebanyakan literatur yang ditulis ahli statistik menggunakan p-value untuk pengujian normalitas. Penerapan p-value pada K-S test adalah jika pengujian signifikan (p < α) artinya data signifikan berbeda dengan kurva normal sehingga data disebut data yang tidak normal distribusinya. Sebaliknya, jika hasil pengujian tidak signifikan (p > α) berarti perbedaan antara data dengan kurva normal tidak signifikan (tidak ada perbedaan antara data dengan kurva normal) yang menyiratkan bahwa data mengikuti distribusi normal.
Pada kasus ini p-value = 0,58 dengan menggunakan level of significance α = 0,05 berarti pengujian tidak signifikan karena p-value = 0,58 > α = 0,05 sehingga dapat disimpulkan bahwa data mengikuti distribusi normal.
Apabila kita menggunakan sebuah ilustrasi maka akan terlihat seperti Gambar 6 di bawah ini dengan area hijau untuk area p-value dan area berarsir merah untuk area α. Data normal jika area hijau lebih luas atau menutupi area α, sebaliknya jika data tidak normal area hijau tidak lebih luas dari area α.
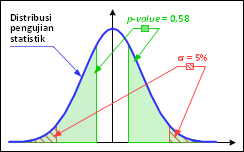
Gambar 6. Pengujian p-value pada level of significance α = 0,05
Simpulan
Profil data yang normal menunjukkan bahwa data tersebut dianggap dapat mewakili populasi. Data berdistribusi normal dapat diamati dari bentuk histogramnya, apakah menyerupai lonceng (kurva normal) atau tidak, tetapi cara ini sangat subyektif, anda dengan pengamat lain mungkin akan mempunyai persepsi yang berbeda. K-S test merupakan uji normalitas yang sederhana dan juga dapat menghindari perbedaan persepsi tersebut.
Kesederhanaan K-S test dipermudah dengan hadirnya software-software pengolah data statistik seperti PSPP yang bebas biaya. Jika anda ragu dengan keakuratan PSPP, anda bisa menggunakan formula-formula yang telah saya uraikan di atas dan membandingkan hasilnya dengan output PSPP. Output K-S test pada PSPP sama persis dengan output SPSS yang mana menghasilkan tiga angka penting, yaitu:
- Nilai-nilai D pada Most Extreme Differences,
- Uji statistik Kolmogorov-Smirnov Z, dan
- P-value yang tercantum dalam Asymp. Sig. (2-tailed).
Saya lebih sering menggunakan angka p-value untuk pengujian, alasannya sederhana karena saya tidak memerlukan bantuan tabel statistik 🙂 . P-value ini lebih akurat untuk uji normalitas karena perhitungannya didasarkan pada pendekatan ke distribusi normal.
Dalam menu Descriptive Statistics –> Explore pada software SPSS, biasanya terdapat K-S Lilliefors test[3] yang merupakan koreksi Hubert W. Lilliefors (1967)[4] terhadap K-S test karena K-S test selama ini tidak dirancang secara khusus untuk uji normalitas. Namun pada PSPP, saya tidak menemukan perintah untuk K-S Lilliefors test. Namun, saya sarankan anda mengkoleksi software ini.
Catatan Kaki:
| [1] | Kolmogorov, A. N. (1933). Sulla determinazione empirica di una legge di distribuzione. Giornale dell’Istituto Italiano degli Attuari, 4, 83–91. |
|
Paper Kolmogorov ini dalam bahasa Italia; terjemahan bahasa Inggris lihat Kolmogorov (1992) dalam daftar rujukan posting ini. |
|
| [2] | Smirnov, N. (1948). Table for estimating the goodness of fit of empirical distributions. The Annals of Mathematical Statistics, 19(2), 279–281. Retrieved from http://www.jstor.org/stable/2236278 |
| [3] | K-S Lilliefors test merupakan modifikasi K-S test karena K-S test tidak bisa digunakan untuk kenormalan jika mean dan standar deviasi (yang diambil dari data sampel) dari hipotesis distribusi normal tidak diketahui. K-S Lilliefors test membandingkan distribusi empiris X dengan distribusi normal dengan mean dan variansi yang sama dengan X. K-S Lilliefors test sama seperti K-S test, namun parameter distribusi normalnya ditaksir dari X. |
| [4] | Lilliefors, H. W. (1967). On the Kolmogorov-Smirnov test for normality with mean and variance unknown. Journal of the American Statistical Association, 62(318), 399–402. Retrieved from http://www.jstor.org/stable/2283970 |
Rujukan:
Biswas, S., Ahmad, S., Molla, M. K. I., Hirose, K., & Nasser, M. (2008). Kolmogorov-Smirnov test in text-dependent automatic speaker identification. Engineering Letter, 16(4), EL_16_4_01. Retrieved from http://www.engineeringletters.com/issues_v16/issue_4/index.html
Brito e Abreu, F., & Goulão, M. (2001). Coupling and cohesion as modularization drivers: Are we being over-persuaded?. In P. Sousa (Ed.), Fifth European Conference On Software Maintenance and Reengineering: 14-16 March Lisbon, Portugal: Proceedings (pp. 47-57 ). Los Alamitos: IEEE Computer Society. doi: 10.1109/.2001.914968
Corder, G. W., & Foreman, D. I. (2009). Nonparametric statistics for non-statisticians: A step-by-step approach. Hoboken, New Jersey: John Wiley & Sons, Inc.
Kolmogorov, A. N. (1992). On the empirical determination of a distribution law. In A. N. Shiryayev (Ed.), Selected Works of A.N. Kolmogorov: Probability Theory and Mathematical Statistics (Vol. 2, pp. 139–146). Dordrecht, Netherlands: Kluwer Academic Publishers.
Massey, F. J. (1951). The Kolmogorov-Smirnov test for goodness of fit. Journal of the American Statistical Association, 46(253), 68–78. Retrieved from http://www.scribd.com/doc/64110324/Kolmogorov-Smirnov-Test-for-Goodness-of-Fit-Massey-1951
Stephens, M.A. (1992). An appreciation of Kolmogorov’s 1933 paper (SOL ONR No. 453). Stanford, California: Department of Statistics, Stanford University.
Yu, H., Zheng, D., Zhao, B. Y., & Zheng, W. (2008). Understanding user behaviour in large-scale video-on-demand systems. In L. Song (Ed.), Innovation together: Microsoft Research Asia academic research collaboration (pp. 125-147). New York: Springer.


Mas apakah ada syarat tertentu untuk memakai 1 sample KS untuk uji normalitas data kita ?
misal n data harus diatas 50 atau dibawah 50.
LikeLike
KS tidak memerlukan data yang dikelompokkan seperti uji chi square sehingga bisa untuk sampel kecil. Namun demikian, semakin besar sampel anda, maka sampel semakin mendekati populasi.
LikeLike
mas kalau saya boleh tanyak, apakah uji normalitas liliefors bisa digunakan untuk parametrik atau untuk nonparametrik
LikeLike
Pak Andi, setahu saya statistik nonparamterik tidak membutuhkan asumsi normalitas. Uji normalitas adalah salah satu uji untuk menentukan apakah data kita nantinya akan dianalisis dengan statistik parametrik atau nonparametrik, jika tidak normal maka kita gunakan statistik non parametrik.
LikeLike
mas, jadi data mentah hasil post test langsung bisa menggunakan uji kolmogorop smirnov, kalau lbh besar dari 0.05 maka normal dan akan dilanjutkan dengan analisis parametrik, tp klw lbh kecil dari 0,05 maka menggunakan nonparametrik: chi square?
LikeLike
pak,saya mau tanya,
bagaimana jika asymp 2tailed saya 0,00005 (yang muncul 0,000)?
sementara dari beberapa referensi yg saya baca asymp 2tailed nya diatas 0,05..
terimakasih
LikeLike
Pak nilai Asymp. Sig. (2-tailed), saya = 1.000
Apakah ini gak salah apa gmna saya bingung
LikeLike
mau tanya kak, nilai Z hitung 1,96 didapat darimana ya?
LikeLike
tabel distribusi normal. Silahkan liat buku statistik
LikeLike
Saya melakukan Pengujian One-Sample Kolmogorov-Smirnov Test, tapi terkendala dengan Asymp. Sig. (2- tailed) lebih kecil dari 0,05. Bagaimana mengatasinya mas?
Hasil yang diperoleh, Asymp. Sig. (2- tailed) = 0,003.
LikeLike